Ground Kinematics
When the car is driving on the ground the user can control their car by accessing the values for throttle, boost and steering. It is import for the bot to be able to calculate the correct amount of each in order to reach a specified target, thus enlies the questions:
- How fast do i need to go to reach a point at a certain time?
- How much do i need to turn in order to reach that point?
- How much boost will i need to use?
- How fast should i be when i reach my target point?
Here I will explain roughly how the car behaves and how I calculated it’s position.
I will be using the units \(\frac{uu}{s}\) which are Unreal Units per second which is the game engines vector magnitudes.
Acceleration
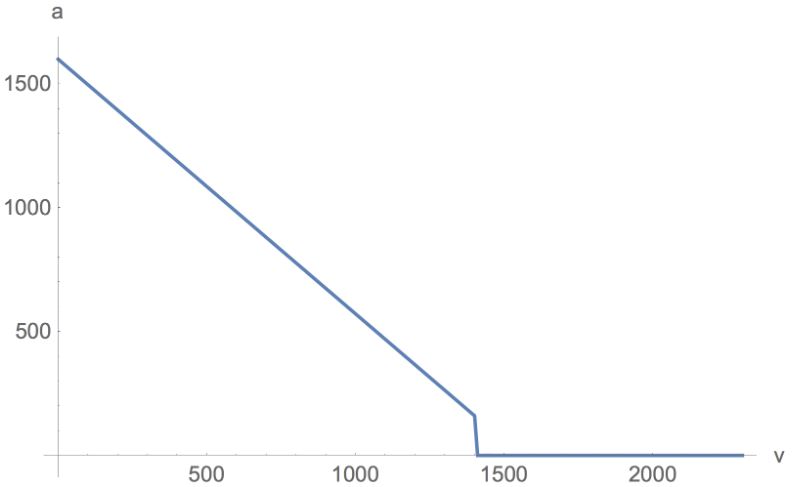
The cars acceleration is entierly dependant on its current velocity, composed of the throttle and boost inputs. It is important to note that the cars acceleration is not constant and does decrease as velocity increases. When the car is at velocity = 0 (at rest) the acceleration is at its greatest and will decrease uniformly to zero when velocity = \(1410 \frac{uu}{s}\)
| Velocity | 0.0 | 1400.0 | 1410.0 | 2300.0 |
|---|---|---|---|---|
| Acceleration | 1600.0 | 160.0 | 0.0 | 0.0 |
The max speed using only the throttle is \(2300 \frac{uu}{s}\)
Braking
In the event that the car’s forward velocity exhibits an opposite sign compared to the input throttle, the car will sustain a constant acceleration of \(3500 \frac{uu}{s^2}\) in the opposing force of motion (against the car) thus slowing the car down.
Coasting
When the car is coasting ie, no throttle or boost input there is constant acceleration of \(525 \frac{uu}{s^2}\) being applied against the car and again slowing it down to a stop.
Boosting
When the boost input is used the cars throttle value is set to a max(\(3500 \frac{uu}{s}\)) and because the car is boosting an additional acceleration of \(991.667 \frac{uu}{s^2}\) will be present.
Gravitational Acceleration
At all times the force of gravity is present, it will have an influcence on the car both in the air and on the ground. In Rocket League the gravity can be calculated as \(g \times f\) where \(g\) is the acceleration of gravity (\(650 \frac{uu}{s^2}\)) and \(f\) is the unit vector along the direction the car is facing.
Credit to Sam Mish for the assisted research